A friend asked me about this problem, on how to calculate the distance an object needs to be from the camera to appear a certain height on the screen.
Easy Solution:
The solution is simpler when dealing with an object centered in the in the screen where a right angle can be created from the camera to the object.
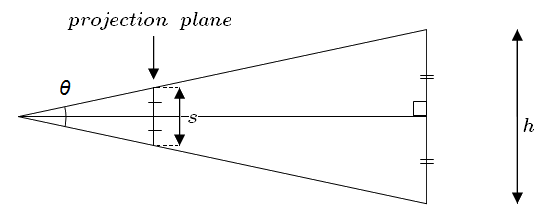
Fig. 1: right angle triangle diagram.
$\figLbl{1}{tanSol}$
Solving the triangle in \ref{fig:tanSol}:
\begin{equation}
\tan{\left( \frac{\theta}{2} \right)} = \frac{h}{2d}
\label{eq:tanTriangle}
\end{equation}
and if you want to solve for the distance $d_{2}$ an object needs to be to appear to be a size $s_{2}$ on the screen, then \eqref{eq:tanTriangle} equation becomes:
$$
\tan{\left(\frac{\theta_1}{2}\right)}\cdot 2d_1 = h = \tan{\left(\frac{\theta_2}{2}\right)}\cdot 2d_{2}\\
$$
\begin{equation}
d_{2} = \frac{\tan{\left(\frac{\theta_1}{2}\right)}}{\tan{\left(\frac{\theta_2}{2}\right)}} \cdot d_1 \\
\label{eq:tanSizeRel1}
\end{equation}
where you can find the values of $\theta_1$ and $\theta_2$ by solving a similar triangle using the size of the object on the screen $s_1$ and its desired new size $s_2$ between the camera and the camera near plane.
\begin{equation}
\theta = 2 \cdot \tan{^{-1}\left(\frac{s}{2 d_{near}}\right)}
\label{eq:tanThetaSol}
\end{equation}
and by subbing \eqref{eq:tanThetaSol} in \eqref{eq:tanSizeRel1}, we get the final solution for $d_2$ in terms of $s_1$, $s_2$ , and $d_1$:
\begin{equation}
d_{2} = \frac{s_1}{s_2} \cdot d_1
\label{eq:tanSolFinal}
\end{equation}
General Solution:
The previous solution only works for object centered on the screen, but nice right-angle solutions don't exist once the object is offset as seen in Fig 2. The solution is still obtainable with some simple high-school math, using either the Sine Law or Cosine Law, and some vector math. Using the Cosine Law gives a better solution, because it gives an unambiguous length solution and we can use the dot product identity $\vec{v_1}\cdot \vec{v_2} = \vert\vert \vec{v_1} \vert\vert$ $\vert\vert\vec{v_2}\vert\vert \cos{(\theta)}$ to get rid of any trigonometric solutions (if we want).
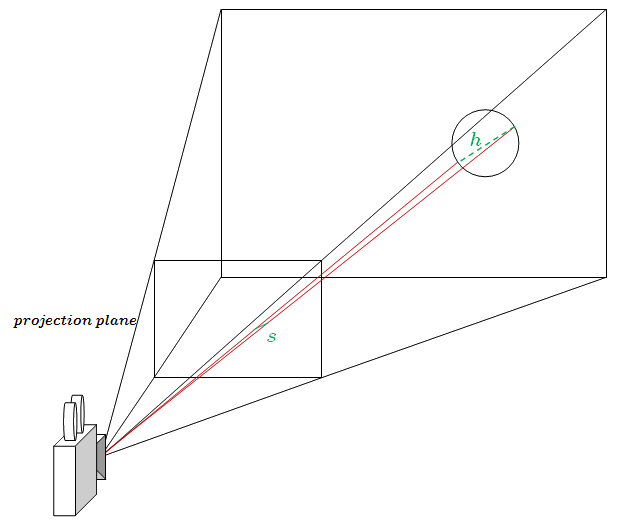
Fig. 2: offset triangle example, object is offset from center giving a cross-sectional triangle without a right-angle.
$\figLbl{2}{cosSolGeneral}$
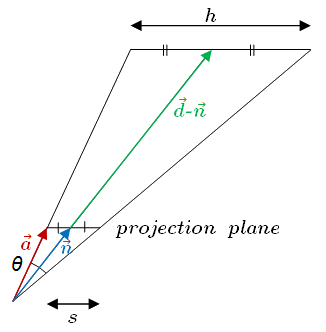
Fig. 3: the 2D triangle representation of the problem in \ref{fig:cosSolGeneral}.
$\figLbl{3}{cosSolTriangle}$
In \ref{fig:cosSolGeneral} and \ref{fig:cosSolTriangle} we have some variables defined, where $h$ and $s$ are the same as the right angle solution, being the size of the object in world space and the size of the object on the screen respectively. We now have vectors, $\vec{d}$ is the distance from the camera to the object, $\vec{n}$ is the distance along $\vec{d}$ to the point of the object on the projection plane of the camera, and a vector that will be important in simplifying our solution $\vec{a}$ is a position on the projection plane offset from $\vec{n}$ by $\left(-\frac{s_x}{2}, -\frac{s_y}{2},0 \right)$
Using the cosine law with respect to $\theta$ in \ref{fig:cosSolTriangle}, we get:
\begin{equation}
\frac{h^2}{4} =\vec{d}^2 + \left( \vec{d}\cdot \hat{a}\hat{a} \right)^2 -2\vert\vert \vec{d} \vert\vert \space \vert\vert \vec{d}\cdot\hat{a}\hat{a}\vert\vert\space \cos{\left( \frac{\theta}{2} \right)}
\label{eg:cosineLaw}
\end{equation}
where we can can make the substitutions:
$$
\left( \vec{d}\cdot \hat{a}\hat{a} \right)^2\\
\Rightarrow \left( \vec{d}\cdot \hat{a}\right)^2 \cancelto{1}{\left(\hat{a} \right)^2}\\
\Rightarrow \vec{d}^2\cancelto{1}{\hat{a}^2}\cos^2{\left(\frac{\theta}{2} \right)}
$$
\begin{equation}
\left( \vec{d}\cdot \hat{a}\hat{a} \right)^2= \vec{d}^2\cos^2{\left(\frac{\theta}{2} \right)}
\label{eq:cosSub1}
\end{equation}
and
$$
\vert\vert \vec{d} \vert\vert \space \vert\vert \vec{d}\cdot\hat{a}\hat{a}\vert\vert\space \cos{\left( \frac{\theta}{2} \right)}\\
\Rightarrow \vert\vert \vec{d} \vert\vert \space\vec{d}\cdot\hat{a}\space \cancelto{1}{\vert\vert\hat{a}\vert\vert\space} \cos{\left( \frac{\theta}{2} \right)}\\
\Rightarrow \vert\vert \vec{d} \vert\vert \space \vert\vert \vec{d} \vert\vert \space \cancelto{1}{\vert\vert \hat{a} \vert\vert}\cos^2{\left( \frac{\theta}{2} \right)}\\
$$
\begin{equation}
\vert\vert \vec{d} \vert\vert \space \vert\vert \vec{d}\cdot\hat{a}\hat{a}\vert\vert\space \cos{\left( \frac{\theta}{2} \right)} = \vec{d}^2 \space \cos^2{\left( \frac{\theta}{2} \right)}
\label{eq:cosSub2}
\end{equation}
and finally,
\begin{equation}
\frac{\vec{a}\cdot\vec{n}}{\vert\vert \vec{a} \vert\vert \space \vert\vert \vec{n} \vert\vert} = \cos{\left( \frac{\theta}{2} \right)} =\hat{a}\cdot \hat{n}
\label{eq:cosSub3}
\end{equation}
Subbing \eqref{eq:cosSub1} and \eqref{eq:cosSub2} into \eqref{eg:cosineLaw}, we get
$$
\frac{h^2}{4} = \vec{d}^2 + \vec{d}^2\cos^2{\left(\frac{\theta}{2} \right)} - 2\vec{d}^2 \space \cos^2{\left( \frac{\theta}{2} \right)} \\
\Rightarrow \frac{h^2}{4} = \vec{d}^2 - \vec{d}^2 \cos^2{ \left( \frac{\theta}{2} \right) } \\
\Rightarrow \frac{h^2}{4} =\vec{d}^2 \left(1 - \cos^2{ \left( \frac{\theta}{2} \right) } \right) \\
\Rightarrow \vec{d}^2 = \frac{ \frac{h^2}{4} } { \left( 1 - \cos^2{ \left( \frac{\theta}{2} \right) } \right) } \\
$$
\begin{equation}
d = \frac{ h }{ 2 \sqrt{ 1 - \cos^2{ \left( \frac{ \theta }{2} \right) } } }
\label{eq:cosSol1}
\end{equation}
subbing in \eqref{eq:cosSub3} into \eqref{eq:cosSol1}:
\begin{equation}
d = \frac{ h }{ 2 \sqrt{ 1 - ( \hat{a}\cdot \hat{n} )^2 } }
\label{eq:cosSol3}
\end{equation}
or converting to full angle variants we can convert \eqref{eq:cosSol1} using trig identities to:
\begin{equation}
d = \frac{ h }{ 2\sin{ \left( \frac{ \theta }{2} \right) } }
\label{eq:cosSol2}
\end{equation}
then using half angle formulas we can convert \eqref{eq:cosSol2} to:
\begin{equation}
d = \frac{ h }{ \sqrt{ 2 \left( 1 - \cos{ \left( \theta \right) } \right) } }
\label{eq:cosSol4}
\end{equation}
